수학2 - 정적분의 기하학적인 의미 설명

정적분의 기하학적 의미 설명입니다.
정적분은 적분을 한 후  적분구간을 이용해서 정적분 값을 구했죠. 그게 유향면적입니다.
면적이긴 한데 방향은 있는?
그러니까 x축보다 밑에 있는 면적은 정적분 하면 음수가 나옵니다.

정적분을 하다보면 0도 나올 수 있고요.

수학2에 막바지에 다 왔습니다.
이제 정적분 부분만 끝나면 그냥 틈틈히 필요한 부분만 하려 합니다 ㅎㅎ

수학2도 이제 공통 부분이라 필수죠.

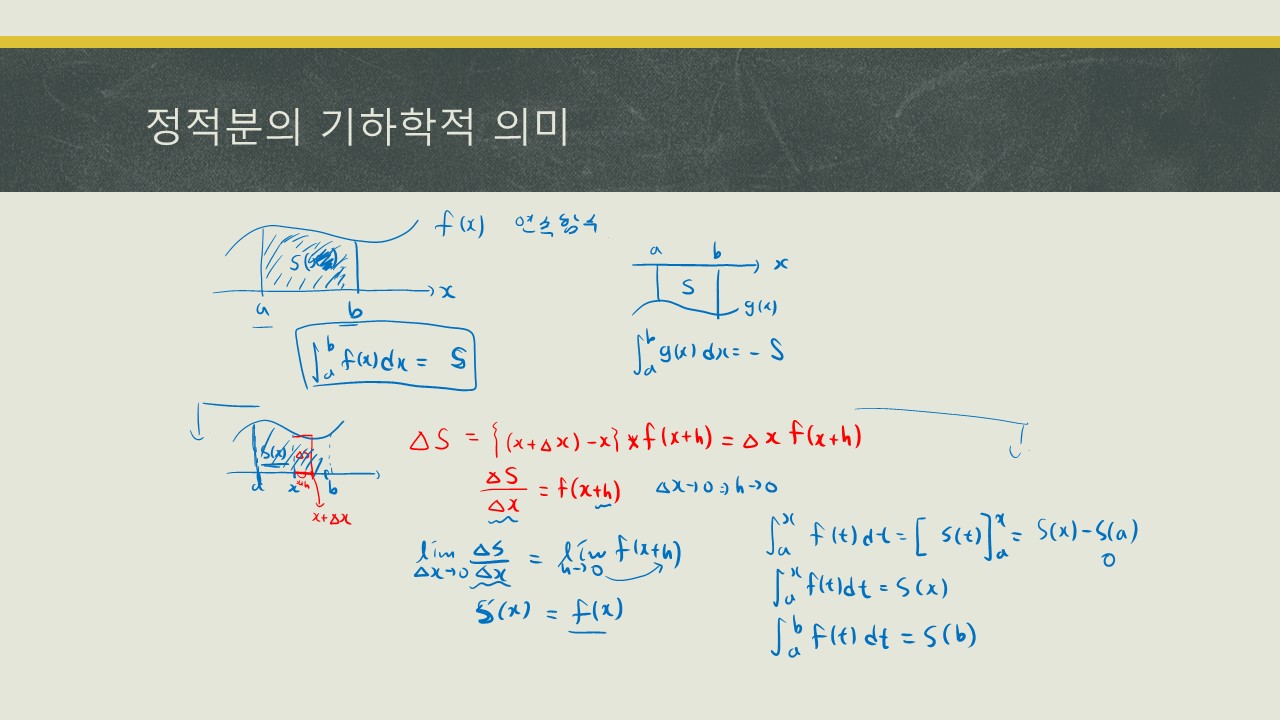
기하학적의미를 살펴봤습니다.
기하학적의미로는 면적이에요.
잘게 잘게 쪼개면 실처럼 됩니다.
그럼 그러한 실들을 구간안에 모아서 보면 면적이 되겠죠?
x축에 밑에 있다면 마이너스 일것 입니다.

구간에 따라 함수가 다를때의 정적분 설명 입니다.
구간이 다른데 그게 사이에 있고 정적분을 구하라고 하면
나눠서 따로따로 정적분을 해야 합니다.
a부터 c까지 정적분해서 구하고 c부터 b까지 정적분 해서 구하고요.
저런식으로 함수가 나눠지면 당연히 정적분은 나눠서 해야하고요. 절댓값 함수도 한개로 써있지만 구간이 나눠진다면 마찬가지로 나눠서 적분해야 합니다.

절댓값 기호가 포함된 정적분 입니다.
절댓값은 x축보다 밑에 있던 함수를 위로 올려주니까 양수가 되죠
그래서 x축보다 밑에 있는 함수따로 위에 있는 함수 따로 정적분을 구해야합니다.
x축 밑에 있는 정적분을 하면 원래 구하려던 값은 음수였을 테니까 마이너스를 붙여줘서 양수로 만들어야 해요.

y축 대칭인 우함수와 원점대칭인 기함수 일때 정적분 하는 방법입니다.
기함수 일때는 쉽습니다. 구간에 절댓값이 같으면 0이에요. 지워주고 계산하면 됩니다.
우함수 일때는 y축 기준으로 왼쪽 오른쪽 대칭이니까 오른쪽만 구하고 2배 해주면 됩니다.

주기함수 대칭함수 정적분 입니다.
주기함수에 대칭함수까지 나왔을 때는
그 구간에 정적분 값을 구해주고 배수를 해주면 되겠습니다.