티스토리 뷰
아래로 볼록 조건 4가지 알아보기

오늘은 아래로 볼록 조건네 가지를 알아보려고 합니다. 수학2나 미적분 과목에 있고요. 그래프를 그릴 때 보통 많이 활용을 하고 그 그래프를 이용해서 어떤 응용 문제를 풀 때 자주 나옵니다. 조건이 주어져 있고 그래프를 정확히 그려야 할 문제들이 모의고사나 수능 같은 유형에서 자주 나옵니다.
미적분에서는 이계도함수를 배우게 됩니다. 그것은 두 번 미분한 형태입니다. 한 번 미분했을 때 도함수가 0이 되고 부호가 바뀔 때 극값이 생겼습니다.
그것과 마찬가지로 두 번 미분한 이계도함수가 0이 되는 점을 찾고 부호가 바뀔 때 변곡점이 생기게 됩니다. 그래서 변곡점을 기준으로 좌우 중에 한곳에서 이계도함수가 음수일 때는 위로 볼록하고요. 이계도함수가 양수일 때는 아래로 볼록하게 됩니다.

아래로 블록에는 네 가지 타입이 있습니다. 첫 번째는 많이 나오는 문제 있는 유형입니다. 조건이 저런식으로 주어져 있을 때 그래프로 밑에 설명을 해 놨으니 참고하시면 되겠고요.
두 번째 거는 미분계수 값과 평균변화율 값이죠. 그래서 두식의 관계가 저럴 때 아래로 볼록합니다. 그리고 세 번째는 위에서 말한 이계도함수가 양수일 때 아래로 볼록합니다. 그리고 네 번째는 자주 안 나오지만 정적분식과 저 옆에 식은 사다리꼴식 입니다 그거 두 식의 관계에서 저런 부등호가 될 때 아래로 볼록하게 됩니다.
아래로 볼록 4가지 타입입니다. 첫번째는 아까 말씀 드렸듯이 중점의 합숫값과 함숫값의 중점의 관계입니다. 어느쪽으로 부등호가 되냐에 따라서 아래로 볼록이나 위로 볼록 아니면 직선이 될 수 있습니다. 두번째는 미분계수와 평균변화율의 관계입니다. 이것도 마찬가지로 부등호 방향에 따라 위로 볼록 아래로 볼록이 나뉘고요.
세번째는 이계도함수 배우면서 변곡점과 함께 아래로 볼록인지 위로 볼록인지를 배웁니다. 이계도함수가 0보다 큰지 작은지에 따라서 위로 볼록 아래로 볼록이고 a에서 0이 되면서 부호가 달라지면 변곡점이 됩니다. 네번째는 위로 볼록 문제에서 자주 나오는 유형은 아니지만 정리해놨습니다. 한번은 나오면 좋겠네요. 정적분한 것과 사다리꼴 넓이와의 관계입니다. 밑에서 이제 자세히 설명할게요.
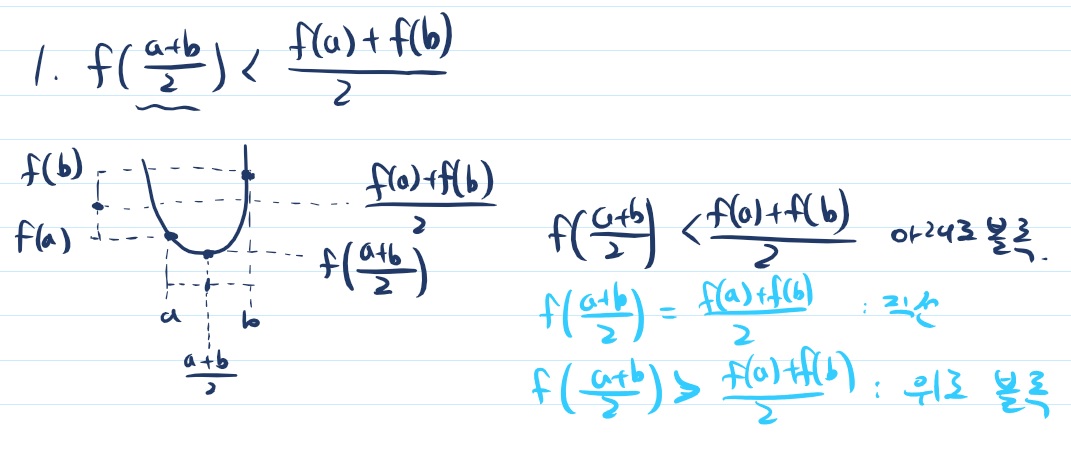
중점의 함숫값이 함숫값의 중점보다 작으면 아래로 볼록입니다. a, b의 중점은 a와 b 가운데에 있겠고 함숫값을 넣는다면 아래로 볼록이기 때문에 더 작을 것입니다. 그것을 아래로 볼록 그래프를 그려서 설명했습니다. 물론 반대로 나오면 위로 볼록이 되겠죠. 그리고 같으면 직선이 될 것 입니다. 이 과정도 색깔별로 정리 해놓은 자료가 있는데 아래로 볼록 네가지 종류를 정리하면서 다시 다뤘습니다.

아래로볼록조건
미분계수와 평균 변화율의 관계입니다. 저기에 추가로 b에서의 미분계수는 제일 크겠죠. 아래로 볼록이라면요. 이 아래로 볼록의 조건은 모의고사에서 자주 나왔던 조건입니다. 그래프를 보시면 아래로 볼록이면 빨간색의 미분계수가 초록색의 평균변화율보다 작은 것을 알 수 있습니다. 그래서 부등식이 왼쪽에 있는 a의 미분계수가 a,b의 평균변화율 보다 더 작다고 나오면 아래로 볼록이고요. a의 미분계수가 b의 미분계수보다 작아도 아래로 볼록이겠죠. a,b의 평균변화율이 b의 미분계수보다 작아도 아래로 볼록 조건 이겠고요. 위로 볼록은 빨간색인 a의 미분계수가 초록색인 a,b의 평균변화율보다 크면 위로볼록입니다.
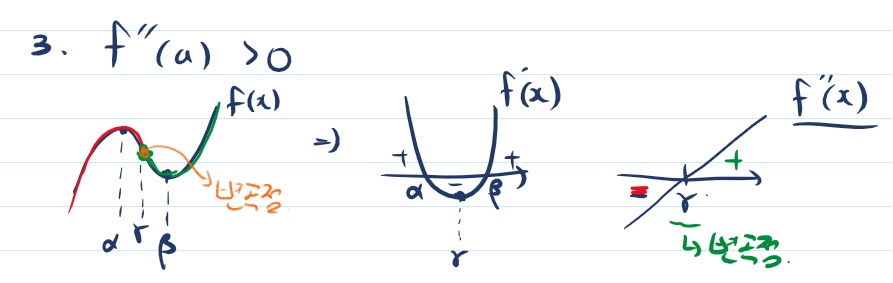
아래로 볼록에서 이계도함수 배울 때 나오는 내용입니다. 변곡점도 같이 설명했습니다. 두번 미분한 그래프에 부호가 바뀌어야 변곡점이 생깁니다. 변곡점은 곡선이 변하는 점인데 위로 볼록에서 아래로 볼록으로 바뀌거나 아래로 볼록에서 위로 볼록으로 바뀌면 그 바뀌는 점에서 변곡점 입니다.
수학2에도 나오는 내용인데 미분을 배우고 도함수를 구할 때 도함수에서 0이 되는 점을 구합니다. 그리고 부호가 바뀌는지 확인하죠. 바뀌면 극값이고 안 바뀌면 극값을 안 갖습니다. 미적분에서 배우는 변곡점도 그것과 마찬가지인데 미분을 두번한 것이 차이점이죠. 두번 미분한 이계도함수에 0이 되는 점을 찾고 부호가 바뀐다면 변곡점을 갖고 부호가 안 바뀌면 변곡점을 안 갖습니다.
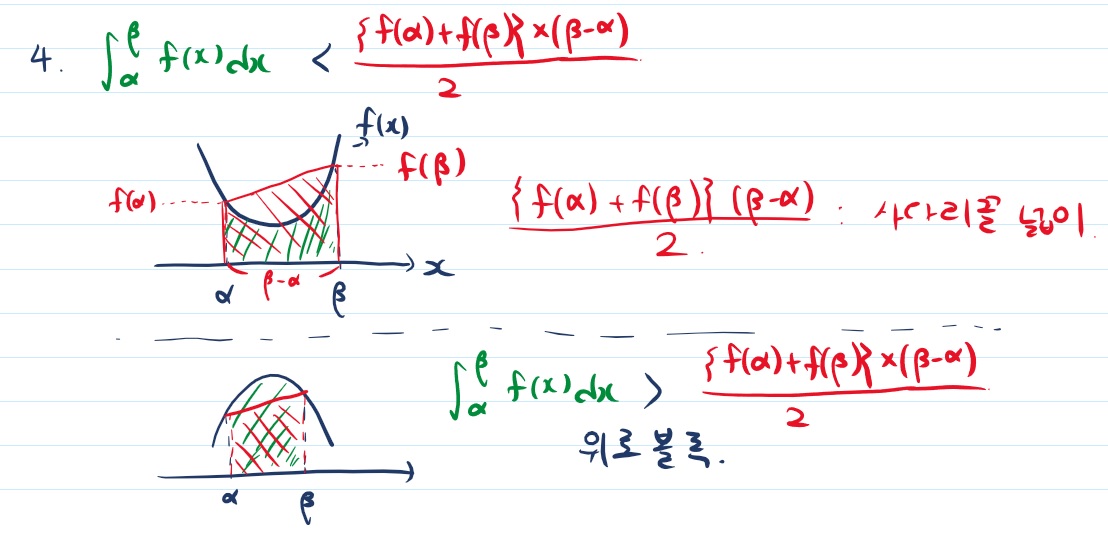
마지막으로 정적분과 사다리꼴의 관계입니다. 초록색으로 표시한 넓이와 빨간색으로 표시한 넓이를 잘 구분하셔야 합니다. 초록색의 넓이는 알파부터 베타까지의 정적분한 값입니다. 그리고 빨간색은 사다리꼴 넓이 공식인 윗변 더하기 아랫변 곱하기 높이 나누기 2를 한 식입니다. 아래로 볼록이라면 사다리꼴이 더 클 수 밖에 없죠.
그래서 네번째에 정적분값이 사다리꼴 넓이보다 작다면 아래로 볼록입니다. 반대는 당연히 정적분 값이 더 클 것이고 위로 볼록이겠습니다.
오늘은 아래로 볼록이 조건으로 나오는 4가지 유형에 대해서 정리해 봤습니다.